Rectas

¿Qué son las rectas paralelas?

Las rectas paralelas son dos o más rectas que se ubican en el mismo plano cartesiano y que nunca intersecan la una con la otra. Sin importar qué tan largo extendamos a dos rectas paralelas, nunca se tocarán.

El siguiente es un diagrama con dos pares de rectas paralelas.

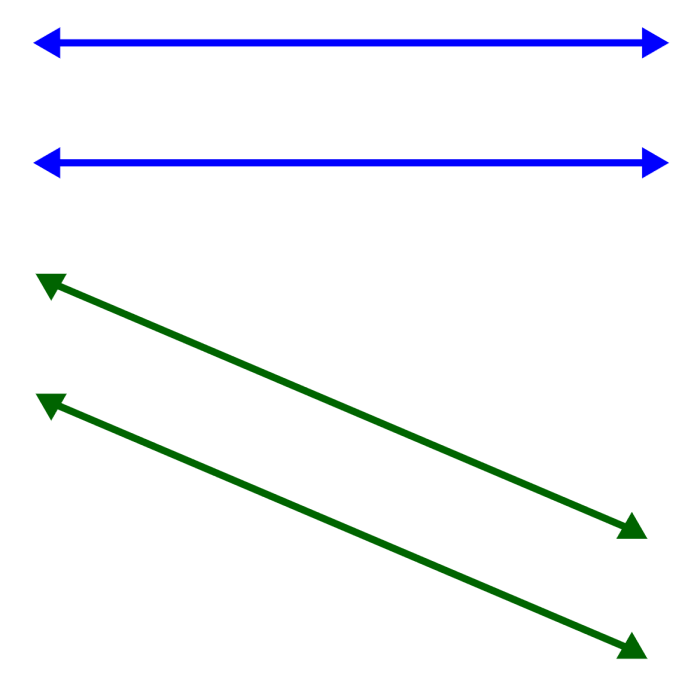
La característica principal de dos o más rectas paralelas es que tienen la misma pendiente. Es decir, el ángulo de inclinación de las rectas paralelas es el mismo.

¿Qué son las rectas perpendiculares?

Las rectas perpendiculares son dos rectas que intersecan la una con la otra en un ángulo de 90°. Es decir, las rectas perpendiculares forman un ángulo recto en su punto de intersección.

El siguiente es un diagrama de dos rectas perpendiculares.

---

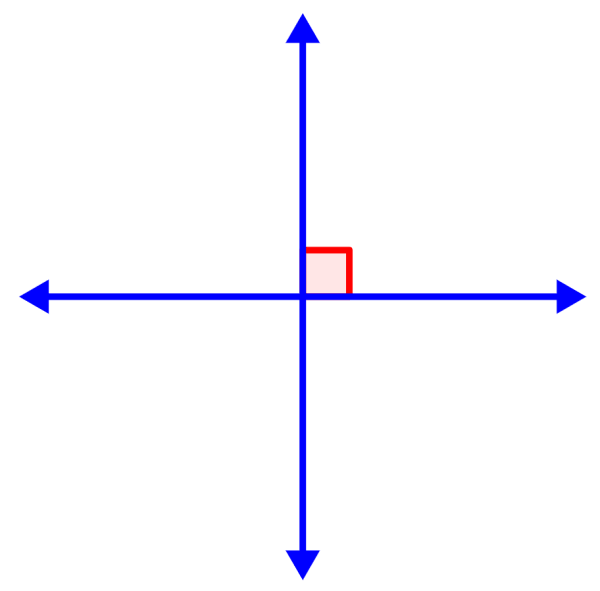
Propiedades de las rectas paralelas y perpendiculares

Las rectas paralelas pueden ser identificadas porque tienen la misma inclinación y nunca se tocan. Por otro lado, las rectas perpendiculares pueden ser identificadas porque forman una intersección con forma de «L».

Las siguientes son algunas propiedades importantes de las rectas paralelas:

• Las rectas paralelas nunca se intersecan la una con la otra.
• La distancia entre dos rectas paralelas siempre se mantiene constante.
• Las pendientes de las rectas paralelas son las mismas.

Las siguientes son algunas propiedades importantes de las rectas perpendiculares:

• Las rectas perpendiculares siempre intersecan la una con la otra.
• El ángulo de intersección entre dos rectas perpendiculares siempre es 90°.
• Las pendientes de las rectas perpendiculares son recíprocas y negativas la una de la otra. Es decir, tenemos ${𝑚}_1=-\frac{1}{{𝑚}_2}$.
• Si es que una recta es perpendicular a una recta que es paralela con otras rectas, entonces, la recta es perpendicular a todas las otras rectas.

---

¿Cómo determinar si dos rectas son paralelas o perpendiculares?

Podemos determinar si dos rectas son paralelas o perpendiculares usando los ángulos formados entre las rectas o usando sus pendientes.

Usar los ángulos formados

Para que dos rectas sean perpendiculares, el ángulo de intersección debe ser igual a 90°. Por otro lado, para que las rectas sean paralelas, el ángulo formado por las rectas con respecto a la horizontal, deben ser iguales.

Usar las pendientes de las rectas

Para que dos rectas sean paralelas, sus pendientes deben ser las mismas. Por otro lado, para que dos rectas sean perpendiculares, sus rectas deben ser recíprocas negativas la una de la otra.

Es decir, para dos rectas que tienen las pendientes ${𝑚}_1$ y ${𝑚}_2$, tenemos:

Paralelas: ${𝑚}_1={𝑚}_2$

Perpendiculares: ${𝑚}_1=-\frac{1}{{𝑚}_2}$

Recordemos que en la ecuación de una recta $𝑦=𝑚𝑥+𝑏$, m es la pendiente.

Además, si es que conocemos dos puntos en la recta, su pendiente es $𝑚=\frac{{𝑦}_2-{𝑦}_1}{{𝑥}_2-{𝑥}_1}$, en donde, $({𝑥}_1,{𝑦}_1)$ y $({𝑥}_2,{𝑦}_2)$ son las coordenadas de los puntos.